FREE MOTION OF A ROTATING CYLINDER UNDER GRAVITY IN A VISCOUS INCOMPRESSIBLE FLUID
AMSURE 2022 with Charles S. Peskin and Leif ristroph
Inspired by a video posted by Veritasium, this project tries to explore the possiblity of using magnus effect as lift of aircraft. In this project, we simulated a rotating cylinder with fixed rotation rate immersed in the viscous incompressible fluid under gravity. Under some rotation rates, we found that the cylinder moves horizontally as the gravity of the cylinder was balanced by the lift force generated by the Magnus effect. By doing multiple runs, we gave out expression for horizontal velocity and the excess mass of the cylinder, the result agrees with the model using standard lift formula.
Presentation: here
SIMULATED FUNGI DECOMPOSITION SYSTEM
with Xiaoyan Tang, Kris Chen compete in The Mathematical Contest in Modeling
In order to incorporate the fluctuations of the environment into our model, we design the Environment Fungi Coefficient Abstraction (EFCA) to quantify the impact of PH, temperature, moisture and light intensity to the fungus communities. We set up the environment index to precisely determine the growth rate, death rate and decomposition rate of the specific fungus community. Based on biological knowledge and mathematical principles, we justify the functions we choose for the three rates are suitable through data fitting and error testing using MATLAB tool packages.
Report: here
NUMERICAL SOLUTION TO THE CONCENTRATION PROFILE OF A GIVEN NEPHRON DENSITY
Final project for Advanced Topics In Math Biology: Physiological Control Mechanisms taught by Charles S. Peskin
Nephron plays a crucial role in the control of the volume and the Na+ concen tration in the extracellular fluid. In this project, we will first describe a single Nephron Model. This model has the limitation that the concentration of the urine cannot be bigger than e times the concentration of the blood plasma. However, there is no such limit in the nephron observed. To address this problem, a more complete multi-nephron model considering the length distribution of the Nephron is presented. To calculate the concentration in the urine, an integral equation is needed to be solved. A numerical scheme was used to solve the resulting integral equation of the model with any Nephron length distribution. The final result shows that given some distributions, the concentration in the urine can be arbitrary high without considering the water flux from the collecting duct. With the flux from the collecting duct being considered, however, the concentration in the urine is signicantly decreased but still larger than e times the concentration in the plasma.
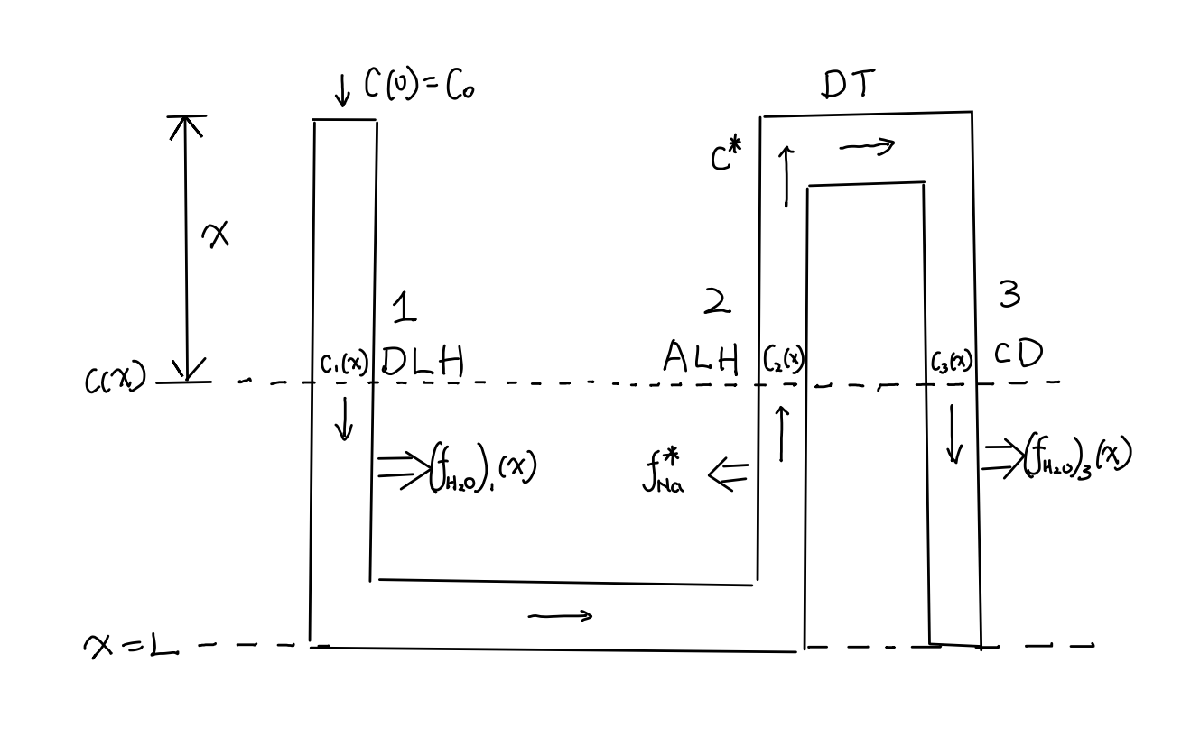
Report: here
MEASUREMENT OF ROTATIONAL TORQUE CAUSED BY A DISSOLVING OBJECT
DURF 2021 with Jinzi Huang
Our project measures the change of torque caused by a hard candy ball of radius 2.4 cm. According to our measurement, the torque the dissolving ball received from the uid can reach 0.1 dyne cm during the whole process of dissolution. Along with the trend over in a smaller time scale, uctuation in the torque with amplitude around 0.01 dyne cm and period about 30- 40 seconds is also observed. Also, by increasing the sugar concentration in the background fluid, the carrying fluctuation amplitude decreases.
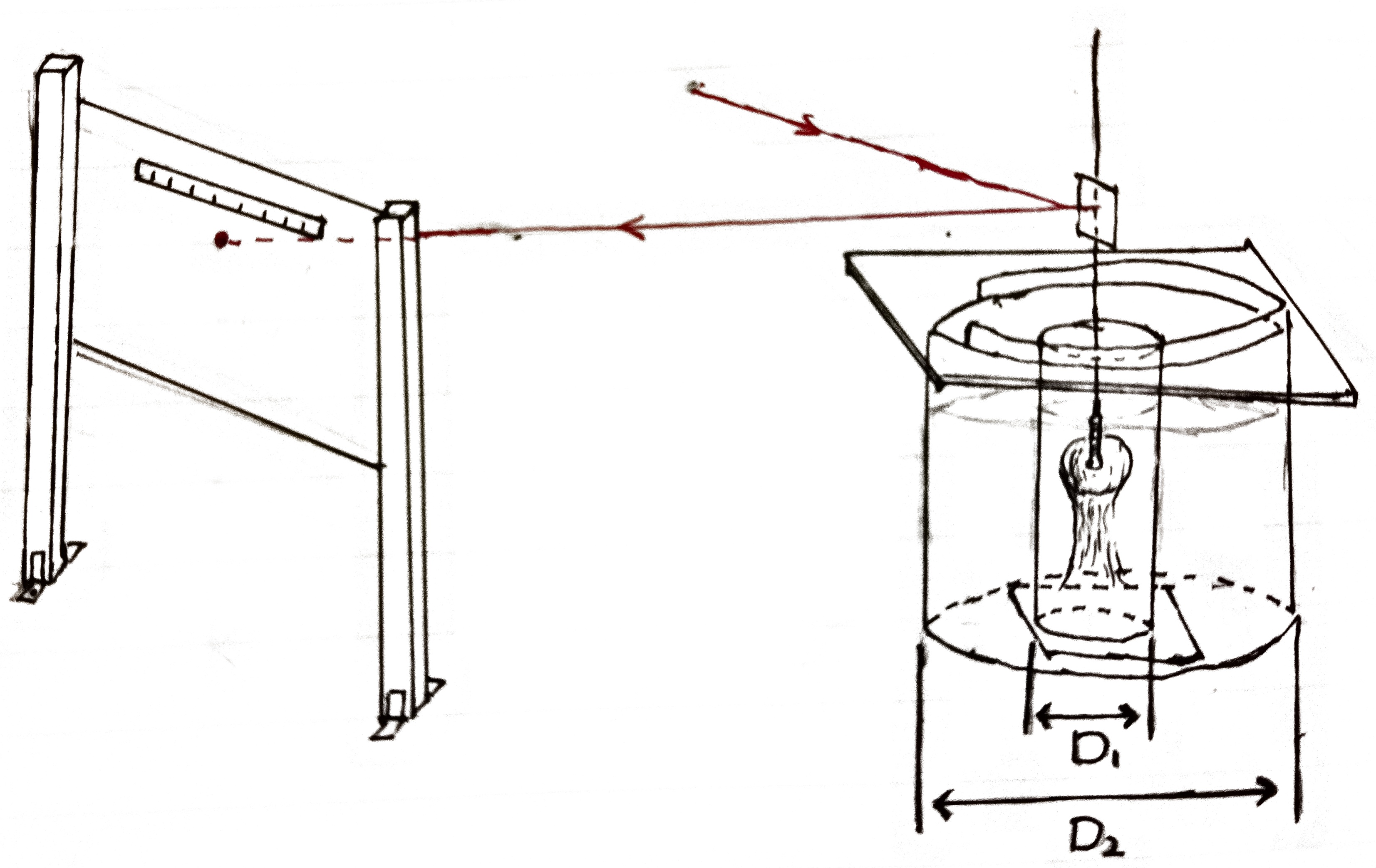
Report: here
A DEMONSTRATION OF PARAMETRIC RESONANCE
Course project of MODELING AND SIMULATION IN SCIENCE, ENGINEERING, AND ECONOMICS thaught by Charles S. Peskin
In this project, we demonstrate the parametric resonance of a 2D elastic ring using the existing implementation of immersed boundary method. The ring is constructed using the zero-length Hookean springs, the ring is immersed in a square domain of fluid. This setup is analogous to a three-dimensional water balloon immersed in water. As for the dimension of the setup, the size of the square is 1 cm times 1 cm, the size of the fingernail. The boundary of the square is periodic, meaning that water flowing up out of the domain will flow into the domain in the bottom again. Similar for the left and right.
Report: here
SIMULATIONS ON ADAPTED THOMSON PROBLEM WITH DIFFERENT FRAMES
Course project of INTRO TO COMUPTER SIMULATION thaught by Charles S. Peskin
Thomson's problem is determined the ground state of N electric charges on constrained in a sphere shell given the repelling effect given by Coulomb's law. By comparing the simulation result and continuum theory, M. Bowick et al. find out the crystalline structure in the ground state for the Thomson problem. In the meanwhile, Y. Levin and J. J. Arenzon generalized the Thomson problem replacing the sphere shell with a sphere. They found that with a small amount of charge, the charges are likely to go to the surface while for a large amount of charge, there are some charges that stay in the middle of the sphere. Our work includes the two-dimensional simulation on the Thomson problem and the three-dimensional simulation on the generalized Thomson problem. While the original Thomson problem assumes on a sphere shell which is a two-dimensional object, we explore the 2d square frame set up. For 3d simulation, the charges are allowed to move inside of the sphere.
Report: here
AN IMPLEMENTATION OF BACKWARD EULER'S METHOD ON SPRING SYSTEM
Course project of MODELING AND SIMULATION IN SCIENCE, ENGINEERING, AND ECONOMICS thaught by Charles S. Peskin
In this project, Backward Euler's method and Forward Euler's method have been implemented and compared in the simulation of the spring system. Forward Euler's method is easier to implement than Backward Euler's method. However, when the stiffness of the spring becomes larger, the method breaks down. Although the Backward Euler's method is harder to implement, it provides ultra stability which can deal with stiffer springs.
Report: here
A SIMPLE SIMULATION FOR MANHATTAN TRAFFIC
Course project of INTRO TO COMUPTER SIMULATION thaught by Charles S. Peskin
In this project, a simple traffic grid is built to mimic the traffic system at Manhattan in New York City. Manhattan has 214 numbered streets and 11 numbered avenues. The streets go in the East-West direction while the avenues go from South-North. The directions here are all aligned with the Hudson River. In real Manhattan, some streets and avenues can go in both directions. To simplify the problem, only alternating direction one-way streets and avenues are considered. The motivation of this project is to have a descriptive model to the Manhattan traffic flow and some qualitative insights about the capacity of the grid system.
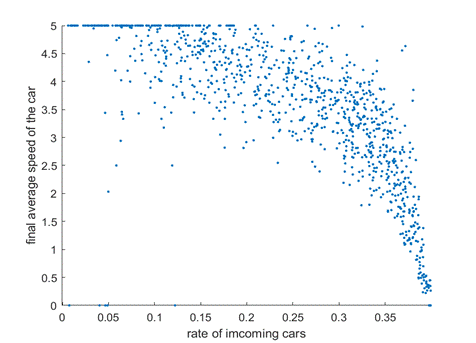
Report: here
COMPARISON BETWEEN NON-DETERMINISTIC MODEL AND DETERMINISTIC MODEL FOR MALARIA AND SICKLE-CELL HEMOGLOBIN GENE
Course project of INTRO TO COMUPTER SIMULATION thaught by Charles S. Peskin
In this project, I explore the long-term behavior of the Sickle-Cell gene and malaria. I first introduce the mathematical model and its implementation in MATLAB. The model has two versions-the deterministic version and the non-deterministic version. I find that with the default value for initial susceptible, infected and resistant, the deterministic model and the non-deterministic model have similar behavior while behave differently when the initial infected population is small. Moreover, as the infection rate of malaria gets larger, the ratio of resistant to malaria also gets larger as the result of natural selection.

Report: here
A MODEL TO PREDICT THE MAXIMUM CAR SPEED IN THE RAIN
Final project of INTRO TO MATH MODELING with Mingming Chen, Liancheng Gong, Xiaoyan Tang, Shuhan Yuan
The speed that a car can maintain on rainy days depends on many factors. This project will first introduce a model to quantify the visibility of the driver using the ratio between the surface area of all raindrops on windshield and the area of the windshield. In addition to driver's comfortability of visibility, we also take the sudden brake, sleep-deprived driving, road condition and light change, into the safe speed consideration. In this project, we build a model to compute the safe speed of the car under real-life considerations by combining mathematical and physical knowledge to provide a concrete and useful insight into this problem.
Report: here
A FLOP COUNT TOOL WITH AN EXAMPLE IN PLU FACTORIZATION
DURF 2020 with Leonardo T. Rolla
We develop a new flop tool which can help to count floating-point operation(flops) in MATLAB/GNU Octave. The first two sections describe the flops and PLU factorization. In the following sections, we introduce the PLU factorization - a method for solving linear equations. We discuss several possible ways to count flops on a PLU factorization script in MATLAB/Octave. One way we tried is using the flop tool developed by Hang Qian. Although his tool does not give us the correct result due to its limitation on counting operations involving varying variable sizes, his code gives the flop count formulas we needed in developing the new tool. Our new tool is compatible with GNU Octave and it is licensed under GNU LGPL.
Report: here
AN OVERVIEW ON LINEAR SOLVERS
DURF 2020 with Leonardo T. Rolla
The Conjugate Gradient Method (CG) is a prevalent method for solving linear systems. In this report, we include a self-contained description of CG and Steepest Descent (SD) without introducing Krylov space. We also describe the preconditioning and its application on CG (PCG). We then compare SD, CG, PCG by considering their iterations. We find that due to roundoff error, the iteration number can go beyond the theoretical upper bound for SD. Finally, we compare those gradient methods with PLU factorization. The resulting linear solver is given in the conclusion part.
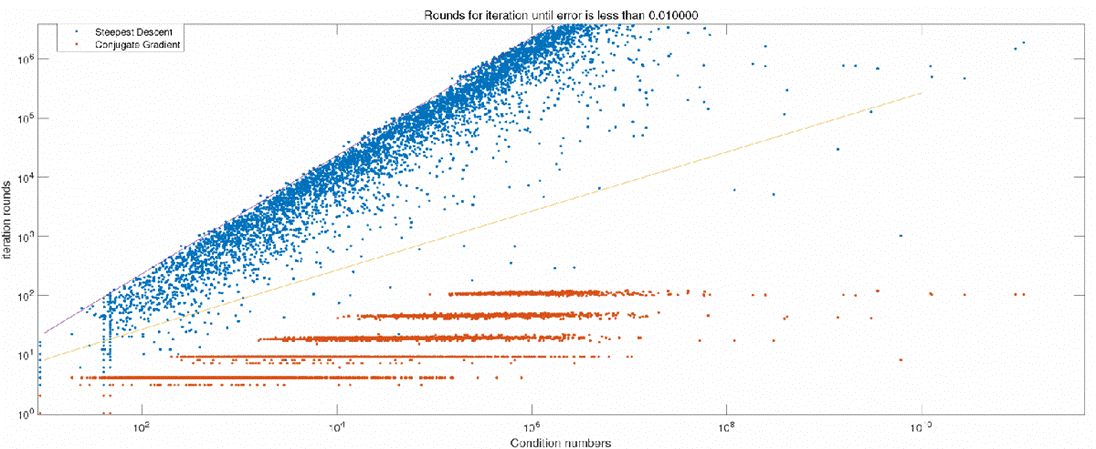
Report: here
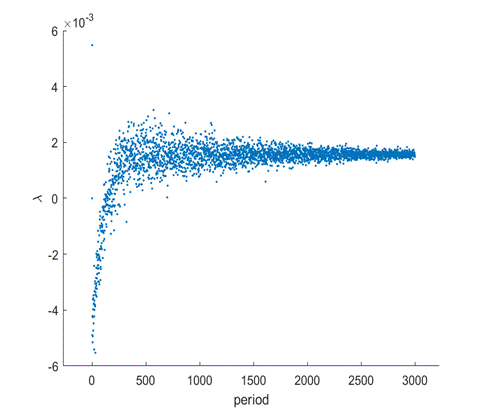
FINDING FEW LARGEST EIGENVALUES
DURF 2020 with Leonardo T. Rolla
Power Method (PM) allows us to find the largest eigenvalue of real square matrices. By changing the algorithm of PM, the resulting algorithm - Inverse Power Method (IPM) enables us to find the eigenvalues other than the largest one. In this report, we firstly describe the IPM and code it in MATLAB/Octave. To test the new function of IPM, we elaborate on how IPM allows us to find eigenvalues closest to a point for symmetric matrices. We then move on to elaborate on how we find the few largest eigenvalues for symmetric matrices using the IPM and the searching scheme we devised. The method succeeded in finding all the 10 largest eigenvalues of 30 by 30 random symmetric positive matrices in 98.4% sampled randomly.
Report: here